이등변 삼각형 넓이 공식 유도, 예시
이등변 삼각형은 두 변의 길이가 같고, 그에 따라 두 각의 크기도 같은 삼각형입니다. 이 단순한 구조 속에는 기하학의 기본 원리와 대칭 개념이 모두 담겨 있습니다. 특히 이등변 삼각형은 넓이 계산이 쉽고, 피타고라스 정리와 삼각비를 이용한 수학적 응용이 다양하여 중·고등학교 수학의 기본 도형으로 자주 등장합니다.
이 글에서는 이등변 삼각형의 넓이 공식 유도 과정을 단계별로 설명하고, 다양한 예시 문제를 통해 공식을 실제로 적용하는 방법을 익히겠습니다. 또한, 각도·변의 길이·높이 등 다양한 조건에서 넓이를 구하는 방식을 모두 다뤄보겠습니다.
이등변 삼각형의 기초 개념
이등변 삼각형의 정의
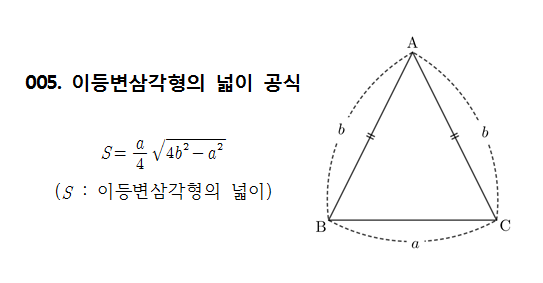
이등변 삼각형은 두 변의 길이가 같고, 그 두 변이 이루는 각이 서로 같습니다.
- 두 변의 길이가 같음: $a = a$
- 밑변은 보통 $b$로 표시
- 꼭짓점에서 밑변에 내린 수선의 길이를 $h$ (높이)라 합니다.
이 수선은 밑변을 정확히 절반으로 나누는 특징이 있습니다. 따라서 밑변의 절반 길이는 $\tfrac{b}{2}$입니다.
구성요소 정리
- 변의 길이: $a, a, b$
- 밑변: $b$
- 높이: $h$
- 꼭짓각: $\theta$
기본 넓이 공식
삼각형의 넓이 공식은 일반적으로
$$
A = \frac{1}{2} \times \text{밑변} \times \text{높이}
$$
입니다.
이등변 삼각형 역시 동일한 방식으로 구할 수 있지만, 이때의 높이 $h$를 피타고라스 정리로 표현할 수 있습니다.
이등변 삼각형 넓이 공식 유도
① 피타고라스 정리를 이용한 유도
이등변 삼각형의 높이 $h$는 밑변을 절반으로 나눈 뒤 피타고라스 정리를 적용하면 구할 수 있습니다.
$$
a^2 = h^2 + \Bigl(\frac{b}{2}\Bigr)^2
$$
이 식을 $h$에 대해 풀면,
$$
h = \sqrt{a^2 – \Bigl(\frac{b}{2}\Bigr)^2} = \sqrt{a^2 – \frac{b^2}{4}}
$$
따라서 넓이 공식은
$$
A = \frac{1}{2} b h = \frac{b}{2} \sqrt{a^2 – \frac{b^2}{4}}
$$
가 됩니다.
이를 조금 단순화하면 다음과 같은 형태도 가능합니다.
$$
A = \frac{b}{4} \sqrt{4a^2 – b^2}
$$
이 공식은 변의 길이만으로 넓이를 구할 수 있는 식입니다.
② 각도를 이용한 유도
이등변 삼각형의 두 변이 $a$, 사이 각이 $\theta$일 때, 삼각함수를 이용한 넓이 공식은 다음과 같습니다.
$$
A = \frac{1}{2} a^2 \sin\theta
$$
이 방식은 높이를 직접 구하지 않아도 되므로, 각이 주어진 문제에서 매우 유용합니다.
③ 헤론의 공식을 이용한 유도
모든 삼각형은 세 변의 길이만 알면 헤론의 공식으로 넓이를 구할 수 있습니다.
이등변 삼각형의 경우에도 적용 가능합니다.
$$
A = \sqrt{s(s-a)(s-a)(s-b)}
$$
여기서 $s$는 반둘레로,
$$
s = \frac{2a + b}{2}
$$
입니다.
이 공식은 세 변의 길이만 주어졌을 때 유용하며, 피타고라스 정리를 쓰지 않아도 됩니다.
이등변 삼각형의 성질
- 두 변의 길이가 같으므로, 두 밑각의 크기가 같습니다.
- 꼭짓점에서 내린 높이는 밑변을 이등분합니다.
- 대칭축을 기준으로 좌우가 완전한 대칭을 이룹니다.
- 외심, 내심, 수심, 방심이 모두 대칭축 위에 존재합니다.
예시 풀이
예시 1. 변의 길이로 넓이 구하기
조건: $a = 10$, $b = 12$
- 높이 구하기
$$
h = \sqrt{10^2 – \Bigl(\frac{12}{2}\Bigr)^2} = \sqrt{100 – 36} = \sqrt{64} = 8
$$ - 넓이 계산
$$
A = \frac{1}{2} \times 12 \times 8 = 48
$$
결과: 넓이 = 48㎠
예시 2. 헤론의 공식 활용
조건: $a = 13$, $b = 10$
- 반둘레
$$
s = \frac{13 + 13 + 10}{2} = 18
$$ - 넓이
$$
A = \sqrt{18(18-13)(18-13)(18-10)} = \sqrt{18 \times 5 \times 5 \times 8} = \sqrt{3600} = 60
$$
결과: 넓이 = 60㎠
예시 3. 각도로 넓이 구하기
조건: $a = 7$, $\theta = 50^\circ$
- 공식 적용
$$
A = \frac{1}{2} a^2 \sin\theta = \frac{1}{2} \times 49 \times \sin 50^\circ
$$
$$
A \approx 24.5 \times 0.7660 = 18.77
$$
결과: 넓이 ≈ 18.77㎠
예시 4. 밑변과 높이로 넓이 구하기
조건: 밑변 $b = 14$, 높이 $h = 9$
$$
A = \frac{1}{2} \times 14 \times 9 = 63
$$
결과: 넓이 = 63㎠
이등변 삼각형의 특수 형태
① 정삼각형의 경우
정삼각형은 세 변의 길이가 같으므로, 이등변 삼각형의 일종입니다.
이때 넓이는
$$
A = \frac{\sqrt{3}}{4} a^2
$$
로 간단히 표현됩니다.
② 직각이등변삼각형
두 변의 길이가 같고, 그 사이 각이 $90^\circ$일 때,
$$
A = \frac{1}{2} a^2
$$
로 계산됩니다.
예를 들어, 변의 길이가 5인 직각이등변삼각형의 넓이는
$$
A = \frac{1}{2} \times 5^2 = 12.5
$$
이등변 삼각형 관련 응용
1. 건축과 구조 설계
이등변 삼각형 구조는 지붕, 교량, 텐트 등의 안정적인 하중 분산 구조로 자주 사용됩니다.
균형 잡힌 형태로, 좌우 하중이 대칭적으로 작용하여 구조적 안정성이 높습니다.
2. 그래픽 디자인
대칭성을 활용한 로고, 패턴, 건축 도면에서도 자주 등장합니다.
정확한 각도와 비율 계산을 위해 위 공식을 적용하면 미적 완성도를 높일 수 있습니다.
3. 수학 교육
삼각형의 넓이, 피타고라스 정리, 삼각비, 사인 공식 등을 통합적으로 가르칠 때 대표 예제로 사용됩니다.
이등변 삼각형의 넓이 공식을 변형하는 방법
- 밑변을 기준으로
$$
A = \frac{1}{2} b h
$$ - 두 변과 각을 기준으로
$$
A = \frac{1}{2} a^2 \sin\theta
$$ - 세 변의 길이만 알고 있을 때
$$
A = \frac{b}{4} \sqrt{4a^2 – b^2}
$$ - 삼각비를 이용한 형태
각도 (\theta)가 주어졌을 때,
$$
h = a \sin\frac{\theta}{2} \times 2
$$
따라서
$$
A = \frac{b}{2} \times a \sin\frac{\theta}{2}
$$
결론
이등변 삼각형은 간단한 구조 속에 수학적 정밀성이 응축된 도형입니다.
밑변과 높이를 이용한 기본 공식뿐 아니라, 변의 길이, 각도, 헤론 공식 등 다양한 방법으로 넓이를 구할 수 있습니다.
각 상황에서 주어진 정보에 따라 알맞은 공식을 선택하면, 계산의 효율과 정확성을 동시에 높일 수 있습니다.
이등변 삼각형은 단순한 도형이지만 기하학·삼각법·물리학적 응용에서 매우 중요한 역할을 하며, 수학의 기본기를 탄탄히 다지는 데 필수적인 도형입니다.
키워드:
이등변삼각형, 넓이공식, 피타고라스정리, 헤론공식, 삼각함수, 삼각형면적, 기하학공식, 수학공식, 공식유도, 예시풀이